
블룸 필터(Bloom Filter) 깊이 알기: 파이썬(Python) 코드와 함께 원리 파헤치기
1. 블룸 필터(Bloom Filter)의 사용 및 적용 시나리오
블룸 필터(Bloom Filter)는 어떤 원소가 특정 집합에 속하는지를 판단하는 데 사용되는, 공간 효율성이 매우 뛰어난 확률적 자료 구조입니다
여러 분야에서 아주 유용하게 활용되고 있는데요
워드 프로세서(Word Processor)의 맞춤법 검사
워드 프로세싱 소프트웨어(word-processing software)에서 영어 단어의 철자가 맞는지 빠르게 검사하는 데 사용될 수 있습니다
예를 들어, 사용자가 단어를 입력했을 때 블룸 필터(Bloom Filter)를 통해 해당 단어가 올바른 단어 집합에 속할 가능성이 있는지 신속하게 판단할 수 있습니다
만약 필터(filter)가 없다고 판단하면, 철자 오류를 사용자에게 알려줄 수 있습니다
에프비아이(FBI) 용의자 명단 조회
에프비아이(FBI)와 같은 기관에서는 특정 용의자의 이름이 이미 용의자 명단에 있는지 빠르게 확인하는 데 블룸 필터(Bloom Filter)를 사용할 수 있습니다
새로운 용의자 정보가 입수되었을 때, 블룸 필터(Bloom Filter)를 이용해 1차적으로 빠르게 스크리닝하여 조사 효율을 높일 수 있습니다
웹 크롤러(Web Crawler)의 URL 방문 여부 판단
웹 크롤러(web crawler)에서는 특정 URL을 이미 방문했는지 효율적으로 판단하는 데 사용될 수 있습니다
이를 통해 같은 URL에 반복적으로 접근하는 것을 방지하고 자원을 절약할 수 있습니다
이메일 스팸 필터링
야후(Yahoo)나 지메일(Gmail)과 같은 이메일 서비스의 스팸 메일 필터링 기능에도 블룸 필터(Bloom Filter)가 활용될 수 있습니다
먼저 특정 기준을 통해 이메일이 스팸일 가능성이 있는지 판단하고, 만약 그렇다고 판단되면 블룸 필터(Bloom Filter)를 거쳐 추가적인 처리를 진행하는 방식입니다
캐시 관통(Cache Penetration) 방지
캐시 시스템(cache system)에서 블룸 필터(Bloom Filter)는 '캐시 관통(cache penetration)' 문제를 방지하는 데 효과적입니다
캐시 관통이란, 캐시(cache)에 존재하지 않는 데이터에 대해 동시에 수많은 요청이 들어와 데이터베이스(database)에 과도한 부하를 주는 현상을 말하는데요
블룸 필터(Bloom Filter)를 사용하면 요청된 데이터가 존재할 가능성이 있는지 먼저 빠르게 확인하고, 만약 존재하지 않을 가능성이 높다면 데이터베이스(database) 조회 없이 바로 요청을 반환하여 불필요한 부하를 막을 수 있습니다
2. 블룸 필터(Bloom Filter) 알고리즘의 장점과 단점
장점
적은 데이터 공간 사용
블룸 필터(Bloom Filter)는 원소 데이터 자체를 저장할 필요가 없습니다
대신 비트 배열(bit array)과 여러 개의 해시 함수(hash function)를 사용하여 데이터의 존재 유무를 표시하기 때문에, 저장 공간을 크게 절약할 수 있습니다
특히 대량의 데이터를 저장해야 할 때, 모든 원소를 직접 저장하는 전통적인 방식과 비교하여 매우 큰 장점을 가집니다
단점
오판 가능성 존재 (False Positive)
블룸 필터(Bloom Filter) 조회 결과가 '없음(Failed match)'으로 나오면 해당 원소는 집합에 "확실히 존재하지 않는다"고 단정할 수 있습니다
하지만 조회 결과가 '있음(Successful match)'으로 나오더라도 해당 원소가 집합에 "확실히 존재한다"고 보장할 수는 없습니다
일정 확률로 '긍정 오류(False Positive)', 즉 실제로는 없는데 있다고 잘못 판단할 가능성이 존재합니다
이는 서로 다른 원소가 여러 해시 함수(hash function)에 의해 매핑(mapping)된 결과, 우연히 비트 배열(bit array)의 같은 위치들을 점유하게 될 수 있기 때문입니다
원소 삭제 불가능
한 번 집합에 추가된 원소는 삭제할 수 없습니다
특정 원소를 나타내는 비트(bit)들을 0으로 되돌리면, 다른 원소들의 존재 유무 판단에도 영향을 미칠 수 있기 때문입니다
원소를 삭제해야 한다면 블룸 필터(Bloom Filter) 자체를 새로 구축해야 합니다
(이를 보완한 카운팅 블룸 필터(Counting Bloom Filter) 같은 변형도 존재합니다)
용량에 따른 긍정 오류율 변화
집합이 거의 가득 차서 추정된 최대 용량에 가까워질수록, 긍정 오류(false positive) 확률은 증가합니다
비트 배열(bit array)에서 1로 설정된 비트(bit)의 수가 많아지면서, 새로운 원소가 추가될 때 이미 1로 설정된 위치에 매핑(mapping)될 확률이 높아지기 때문입니다
데이터 규모에 따른 공간 증폭
일반적으로 1% 정도의 긍정 오류율(false positive probability)을 목표로 할 때, 각 원소당 약 10비트(bit) 미만의 공간이 필요하며, 이는 집합 내 원소의 크기나 개수와는 비교적 무관합니다
비록 상대적으로 공간 효율적이긴 하지만, 데이터 규모가 매우 커지면 전체적으로 차지하는 공간 역시 무시할 수 없을 정도로 커질 수 있습니다
상대적으로 느린 조회 과정
여러 개의 해시 함수(hash function)를 사용하기 때문에, 원소의 존재 유무를 확인하는 각 조회 과정마다 여러 개의 비트(bit)(해시 함수 개수만큼)를 확인해야 합니다
이로 인해 단일 해시 조회 등에 비해 조회 과정이 상대적으로 느릴 수 있습니다
3. 원리 소개
알고리즘 원리
블룸 필터(Bloom Filter)는 어떤 집합에 특정 원소가 포함되어 있는지를 판단하는 알고리즘입니다
데이터 자체를 저장하는 대신, 아주 긴 비트 배열(bit array)과 여러 개의 독립적인 해시 함수(hash function)를 통해 구현됩니다
비트 배열(bit array)의 길이를 (m), 해시 함수(hash function)의 개수를 (k)라고 가정해 봅시다
먼저, 비트 배열(bit array)의 모든 비트(bit)를 0으로 초기화합니다
어떤 원소를 집합에 추가할 때는, 입력된 원소(예: 문자열)를 (k)개의 해시 함수(hash function) 각각에 통과시켜 (k)개의 해시 값(hash value)을 얻습니다
이 해시 값(hash value)들은 비트 배열(bit array)의 인덱스(index) 또는 위치(subscript)에 해당하며, 이 (k)개의 위치에 있는 비트(bit) 값을 모두 1로 설정합니다
만약 동일한 원소를 다시 추가하려고 해도, 같은 해시 함수(hash function)들은 항상 같은 위치를 가리키므로 비트(bit) 값은 여전히 1로 유지됩니다
어떤 원소가 집합에 존재하는지 조회할 때는, 추가할 때와 동일한 (k)개의 해시 함수(hash function)를 사용하여 해당 원소를 비트 배열(bit array) 위의 (k)개 위치로 매핑(mapping)합니다
이때, (k)개의 위치 중 단 하나라도 비트 값이 0이라면, 해당 원소는 집합에 "확실히 존재하지 않는다"고 판단할 수 있습니다
반대로, 만약 (k)개의 위치에 있는 비트(bit) 값이 모두 1이라면, 해당 원소는 집합에 "존재할 수도 있다"고 판단합니다
여기서 '존재할 수도 있다'고 표현하는 이유는 앞서 설명한 긍정 오류(false positive) 가능성 때문이며, 반드시 존재한다고 확신할 수는 없습니다
그림 예시 설명
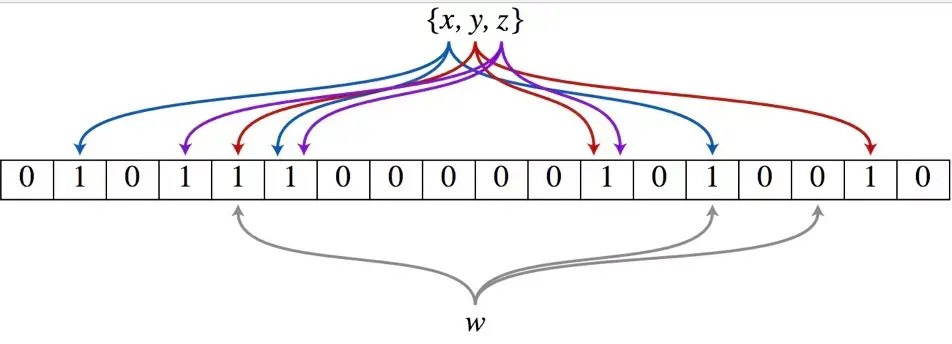
예를 들어, 집합에 3개의 원소 ({x, y, z})가 있고, 3개의 해시 함수(hash function)를 사용한다고 가정해 보겠습니다
집합의 각 원소 x, y, z를 순서대로 3개의 해시 함수(hash function)에 통과시켜 각각 3개의 비트 배열(bit array) 위치를 얻고, 해당 위치들을 1로 표시합니다
이제 새로운 원소 (W)가 집합에 있는지 조회한다고 해봅시다
원소 (W)를 동일한 3개의 해시 함수(hash function)에 통과시켜 비트 배열(bit array) 상의 3개 위치(예: 4번, 8번, 11번)를 얻습니다
만약 이 3개 위치 중 하나라도 0이라면, 원소 (W)는 집합에 확실히 없습니다
그런데 만약 조회 결과 3개 위치(예: 4번, 5번, 6번)가 모두 1이라고 가정해 봅시다
그림을 보면, 4번 위치는 원소 x에 의해 1이 되었고, 5번 위치는 원소 y에 의해, 6번 위치는 원소 z에 의해 1이 되었을 수 있습니다
즉, 원소 (W) 자체는 집합에 없지만, 다른 원소들에 의해 해당 위치들이 우연히 모두 1이 된 경우입니다
이것이 바로 긍정 오류(false positive)가 발생하는 원리입니다
간단한 파이썬(Python) 구현 예제
아래 코드는 블룸 필터(BloomFilter)의 기본적인 개념을 보여주는 파이썬(Python) 구현 예시일 뿐입니다
실제 블룸 필터(BloomFilter) 구현에서는 초기화된 비트 배열(bit array)의 길이에 따라 적절한 해시 함수(hash function)의 개수를 결정해야 하며, 더 정교한 해싱(hashing) 과정이 필요합니다
#_*_coding:utf_8_
# 필요한 라이브러리 설치: pip install bitvector
try:
import BitVector
except ImportError:
print("BitVector 라이브러리가 필요합니다. 'pip install bitvector' 명령어로 설치해주세요.")
# 예제 실행을 위해 간단한 대체 구현 (실제 사용에는 BitVector 권장)
class BitVector:
def __init__(self, size):
self._size = size
self._vector = bytearray((size + 7) // 8)
def __setitem__(self, index, value):
if not (0 <= index < self._size):
raise IndexError("BitVector index out of range")
byte_index = index // 8
bit_index = index % 8
if value:
self._vector[byte_index] |= (1 << bit_index)
else:
self._vector[byte_index] &= ~(1 << bit_index)
def __getitem__(self, index):
if not (0 <= index < self._size):
raise IndexError("BitVector index out of range")
byte_index = index // 8
bit_index = index % 8
return (self._vector[byte_index] >> bit_index) & 1
def __str__(self):
# 간단한 문자열 표현 (디버깅용)
return bin(int.from_bytes(self._vector, 'big'))[2:].zfill(self._size)
import os
import sys
# 간단한 해시 함수 클래스
class SimpleHash():
def __init__(self, cap, seed):
self.cap = cap # 해시 결과의 최대값 (비트 배열 크기)
self.seed = seed # 해시 계산에 사용될 시드 값
def hash(self, value):
ret = 0
for i in range(len(value)):
# 가중치 합 방식으로 해시 값 계산
ret += self.seed * ret + ord(value[i])
# 비트 연산(&)을 통해 최종 해시 값이 0과 self.cap-1 사이에 오도록 보장
return (self.cap - 1) & ret
# 블룸 필터 클래스
class BloomFilter():
def __init__(self, BIT_SIZE=1 << 25): # 기본 비트 배열 크기 설정 (2^25)
self.BIT_SIZE = BIT_SIZE
# 여러 개의 해시 함수를 만들기 위한 시드(seed) 값들
self.seeds = [5, 7, 11, 13, 31, 37, 61]
# 지정된 크기의 비트 배열(BitVector) 생성
self.bitset = BitVector.BitVector(size=self.BIT_SIZE)
# 해시 함수 객체들을 저장할 리스트
self.hashFunc = []
# 시드(seed) 값들을 사용하여 여러 개의 SimpleHash 객체 생성 및 리스트에 추가
for i in range(len(self.seeds)):
self.hashFunc.append(SimpleHash(self.BIT_SIZE, self.seeds[i]))
# 생성된 해시 함수 객체들 확인 (디버깅용)
# print(f"사용될 해시 함수 개수: {len(self.hashFunc)}")
# 원소를 블룸 필터에 추가하는 메서드
def insert(self, value):
# 각 해시 함수를 사용하여 위치(loc) 계산
for f in self.hashFunc:
loc = f.hash(value)
# 해당 위치의 비트를 1로 설정
self.bitset[loc] = 1
# 비트셋 상태 확인 (디버깅용)
# print(f"'{value}' 삽입 후 비트셋 일부: {str(self.bitset)[:100]}...") # 너무 길어서 일부만 출력
# 원소가 블룸 필터에 (아마도) 존재하는지 확인하는 메서드
def is_contaions(self, value): # 메서드 이름에 오타가 있네요. is_contains가 맞을 것 같습니다.
if value == None:
return False
ret = True
# 각 해시 함수로 계산된 위치의 비트 값을 확인
for f in self.hashFunc:
loc = f.hash(value)
# 해당 위치의 비트 값과 현재 결과(ret)를 AND 연산
# 하나라도 0이면 최종 결과는 False가 됨
ret = ret & self.bitset[loc]
return bool(ret) # 결과를 boolean 타입으로 반환
# --- 블룸 필터 사용 예시 ---
bf = BloomFilter()
# 데이터 추가
bf.insert("apple")
bf.insert("banana")
bf.insert("grape")
# 존재 여부 확인
print(f"'apple' 존재 여부: {bf.is_contaions('apple')}") # True 예상
print(f"'orange' 존재 여부: {bf.is_contaions('orange')}") # False 예상 (확실히 없음)
print(f"'watermelon' 존재 여부: {bf.is_contaions('watermelon')}") # False일 수도, True(긍정 오류)일 수도 있음
위 코드에서 SimpleHash 클래스(class)는 간단한 해시 함수(hash function)를 구현하고, BloomFilter 클래스(class)는 비트 배열(bit array)과 여러 개의 해시 함수(hash function)를 초기화하여 원소 삽입 및 존재 여부 판단 기능을 제공합니다insert 메서드(method)는 원소를 블룸 필터(Bloom Filter)에 삽입하는 데 사용되고, is_contaions 메서드(method)(원래는 is_contains가 더 적절한 이름일 것 같습니다)는 원소가 블룸 필터(Bloom Filter)에 존재하는지 (존재할 가능성이 있는지) 판단하는 데 사용됩니다
'Python' 카테고리의 다른 글
| 파이썬(Python) 최강의 기술, 데코레이터(Decorator) 완전 정복 (0) | 2025.05.17 |
|---|---|
| 파이썬 메타프로그래밍 마스터하기: 원하는 모든 것을 제어하는 방법 (0) | 2025.05.06 |
| ASGI 깊이 알기: 파이썬 비동기 웹 앱 통신 규약 파헤치기! (FastAPI, Uvicorn 연관성 포함) (1) | 2025.05.06 |
| 파이썬 리스트 정렬의 숨겨진 비밀: 팀소트(Timsort)는 왜 빠를까요? (0) | 2025.05.05 |
| 파이썬 함수형 프로그래밍 완전 정복: 핵심 원리부터 `map`, `filter`, `reduce` 활용법까지 깔끔 정리! (0) | 2025.04.27 |

